SOURCE CODE ( )
)
' ============================================================================
' INITIALIZATION / INIZIALIZZAZIONE
' ============================================================================
' Let's start measuring the execution time from the first useful instruction.
' Then we also measure the time it takes to initialize the graphics subsystem
' and clear the screen.
'
' Iniziamo la misurazione del tempo di esecuzione dalla prima istruzione utile.
' Quindi misuriamo anche il tempo che impiega a inizializzare il sottosistema
' grafico e a cancellare lo schermo.
'
t=TI
' With this command we ask ugBASIC to select a "bitmap" mode (ie where it is
' possible to draw "pixel by pixel") resolution of preference. In the specific
' case, a resolution of 320 pixels wide by 200 pixels height, for a maximum
' of two colors per pixel, is requested. This request must be understood as a
' suggestion: it is possible that the hardware on which the program will run
' may not have this resolution, or perhaps the minimum number of colors
' is 16. It will be the programmer's responsibility to adapt the program so
' that it can work in every situation.
'
' Con questo comando chiediamo a ugBASIC di selezionare una modalità "a bitmap"
' (cioè dove sia possibile disegnare "pixel per pixel"), con una risoluzione di
' preferenza. Nel caso specifico, una risoluzione di 320 pixel di larghezza
' per 200 pixel di altezza, per un massimo di due colori per pixel. Questa
' richiesta deve essere intesa come un suggerimento: è possibile che l'hardware
' su cui girerà il programma non possa disporre di questa risoluzione, o
' magari il numero di colori minimo è 16. Sarà responsabilità del programmatore
' adattare il programma affinché possa funzionare in ogni situazione.
'
BITMAP ENABLE(320,200,2)
' Let's set the black color for the pixels to be drawn.
'
' Impostiamo il colore nero per i pixel da disegnare.
'
INK BLACK
' Let's clear the screen, setting the background color as white.
'
' Cancelliamo lo schermo, impostando il colore di sfondo come bianco.
'
CLS WHITE
' Now let's calculate the size of the window (screenWidth x screenHeight pixels)
' within which we will draw the Sierpinski triangle. As a general rule, we will
' use a window of 256 pixels wide by a height equal to the maximum that can be
' represented by the hardware. If there are fewer than 256 pixels available,
' we'll use those. If there are more than 256 pixels available, the triangle
' will be centered on the screen (by using and offset of offsetX pixels).
'
' |----------- screenWidth -----------|
' +-------------------------------------------------------+
' |<------->+-----------------------------------+<------->|---
' | offsetX | | offsetX | |
' | | | | | screenHeight
' . . . . .
'
' Ora calcoliamo le dimensioni della finestra entro la quale disegneremo il
' triangolo di Sierpinski (screenWidth x screenHeight pixels). Come regola
' generale, utilizzeremo una finestra di 256 pixel di larghezza per una
' altezza pari al massimo rappresentabile dall'hardware. Se vi sono meno di
' 256 pixel disponibili, useremo quelli. Se vi sono più di 256 pixel
' disponibili, il triangolo sarà centrato sullo schermo (con un offset
' pari a offsetX pixel).
'
CONST screenWidth = IF(SCREEN WIDTH < 256, SCREEN WIDTH, 256)
CONST screenHeight = SCREEN HEIGHT
CONST offsetX = IF(SCREEN WIDTH < 256, 0, ( SCREEN WIDTH - screenWidth ) \ #2)
' The procedure for drawing the triangle requires three (starting)
' coordinates, which are the vertices of the triangle to start from.
'
' * (x1,y1)
' / \
' / \
' (x2,y2) *-----* (x3,y3)
'
' La procedura per disegnare il triangolo necessita di tre coordinate
' (di partenza), che sono i vertici del triangolo da cui partire.
'
CONST x1=(screenWidth\#2): CONST y1=0
CONST x2=0: CONST y2=(screenHeight-1)
CONST x3=(screenWidth-1): CONST y3=(screenHeight-1)
' In order to ensure as "rectangular" distribution as possible of the points
' chosen randomly, we generate an array of 256 elements.
' This map is used as a "lookup table": at the input we have the random
' number (which does have a irregular distribution) and at the
' output we have a distribution of the abscissa of a rectangular type
' (about 33% for each abscissa).
'
' Thanks to Antonio Savona for the suggestion.
'
' 0 ...... 256
' +------------+ +------------+ +----+----+----+
' | | | | | | | x1 | x2 | x3 |
' | ||| ||| || | ======> | xx(..) | ======> +----+----+----+
' ||||||||| |||| | | | 34%| 33%| 33%|
' +------------+ +------------+ +----+----+----+
'
' Al fine di garantire una distribuzione il più possibile "rettangolare"
' dei punti scelti casualmente, si è adottata la scelta di generare un
' array di 256 elementi. Tale mappa viene utilizzata come una
' "tabella di lookup": in ingresso abbiamo il numero casuale (che
' non ha una distribuzione rettangolare) e in uscita abbiamo una
' distribuzione delle ascisse di tipo rettangolare (circa 33% per
' ogni ascissa).
'
' Ringrazio Antonio Savona per il suggerimento.
'
DIM xx AS BYTE(256) = # { _
x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, _
x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, _
x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, _
x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, _
x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, _
x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, _
x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, _
x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, _
x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, _
x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, _
x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, _
x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, _
x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, _
x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, _
x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, _
x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1, x2, x3, x1 _
} READONLY
' See above / Si veda sopra.
'
DIM yy AS BYTE(256) = # { _
y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, _
y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, _
y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, _
y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, _
y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, _
y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, _
y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, _
y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, _
y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, _
y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, _
y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, _
y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, _
y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, _
y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, _
y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, _
y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1, y2, y3, y1 _
} READONLY
' We set the number of points to draw, at most. The challenge includes 10,000 points.
' The greater the number of points, the more defined the triangles will be.
' We also calculate the value of a quarter of the points, as the algorithm will
' draw four points at a time.
'
' Impostiamo il numero di punti da disegnare, al massimo. La challenge prevede 10.000
' punti. Maggiore è il numero di punti, più definiti saranno i triangoli.
' Calcoliamo anche il valore di un quarto dei punti, in quanto l'algoritmo disegnerà
' quattro punti alla volta.
'
CONST limit = 10000
' We define the coordinates of each point as (x, y). These coordinates will be updated
' as the triangle is drawn. The starting value coincides with the top vertex.
'
' Definiamo le coordinate di ogni punto come (x, y). Tali coordinate saranno aggiornate
' man mano che sarà disegnato il triangolo. Il valore iniziale coincide con il
' vertice superiore.
'
x = #x1 AS POSITION
y = #y1 AS POSITION
' This variable keeps the number of points drawn so far.
'
' Questa variabile mantiene il numero di punti disegnati fino a questo momento.
'
n = #0 AS INTEGER
' Starting from this point we start the loop to draw the triangle.
' It is a loop that will be repeated for the total number of points
' to be drawn.
'
' A partire da questo punto iniziamo il loop per disegnare il triangolo.
' Si tratta di un loop che sarà ripetuto per il numero di punti da
' disegnare, complessivamente.
'
REPEAT
' We randomly choose one of the vertices from which to start to draw
' the next point. As explained in the data flow diagram, the choice
' starts from a number ranging from 0 to 255, the distribution of
' which is not completely random.
'
' Scegliamo a caso uno dei vertici da cui partire per disegnare il
' prossimo punto. Come spiegato nel diagramma di flusso dei dati,
' la scelta parte da un numero che va da 0 a 255, la cui distribuzione
' non è completamente causale.
'
r = RANDOM BYTE
' If we were directly based on this number to decide which vertex to start
' from, we would have vertices that would be chosen more frequently than
' the others. This would result in a less defined image on the less
' chosen points. To avoid this, we will use a large vector exactly like
' the number of random numbers that can be generated. This vector contains,
' in an equidistributed way, the information on the acissa and the ordinate
' of each vertex. Once chosen, this coefficient will be added to the current
' coordinates, thus making the average. ugBASIC allows you to use syntax in
' "prefix" form, ie where one of the operands is also the recipient of the
' result of the operation. This is the meaning of the subsequent operations,
' which update the coordinates to be drawn.
'
' Se ci basassimo direttamente su questo numero per decidere da quale
' vertice partire, avremmo dei vertici che sarebbero scelti con maggior
' frequenza degli altri. Ciò determinerebbe una immagine meno definita sui
' punti meno scelti. Per evitarlo, utilizzeremo un vettore grande esattamente
' come il numero di numeri casuali generabili. Tale vettore contiene, in
' modo equidistribuito, le informazioni sull'acissa e sull'ordinata di ogni vertice.
' Una volta scelto, tale coefficiente sarà aggiunto alle coordinate attuali,
' facendone quindi la media. ugBASIC consente di utilizzare sintassi in forma
' "prefissa", cioè dove uno degli operandi è anche il destinatario del risultato
' dell'operazione. Questo è il significato delle operazioni successive,
' che aggiornano le coodinate da disegnare.
'
' x = ( x + xx() ) / 2
' => x = x + xx(); x = x / 2
ADD x, xx(r) : DIV x, #2
ADD y, yy(r) : DIV y, #2
' Finally we can draw the point thus obtained.
'
' Finalmente possiamo disegnare il punto così ricavato.
'
PLOT offsetX + x, y
' Pass to next point.
'
' Passiamo al prossimo punto.
'
INC n
' We repeat the loop until we have drawn all the points.
'
' Ripetiamo il loop fino a che non abbiamo disegnato tutti i punti.
'
UNTIL n = limit
' At the end we calculate how much time has passed, and show
' it on the screen. Rounding is to the second.
'
' Al termine calcoliamo quanto tempo è passato, e mostriamolo
' a schermo. L'arrotondamento è al secondo.
te = TI - t
HOME
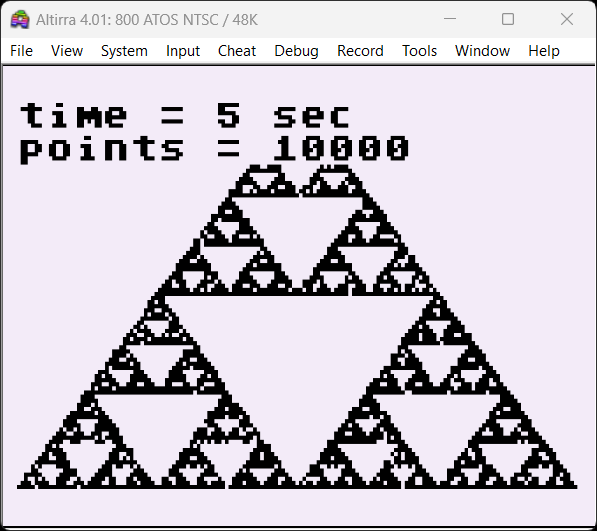
PRINT "time = ";(te/TICKS PER SECOND);" sec"
PRINT "points = ";limit